I’m waitin’ for the time when I can get to Arizona, cause my money’s spent on the goddamn rent
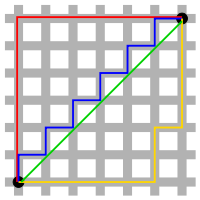
Taxicab geometry, considered by Hermann Minkowski in the 19th century, is a form of geometry in which the usual metric of Euclidean geometry is replaced by a new metric in which the distance between two points is the sum of the (absolute) differences of their coordinates.
The taxicab metric is also known as Manhattan distance, or Manhattan length, with corresponding variations in the name of the geometry. The latter names allude to the grid layout of most streets on the island of Manhattan, which causes the shortest path a car could take between two points in the city to have length equal to the points’ distance in taxicab geometry.


